17CS62 - COMPUTER GRAPHICS AND VISUALIZATION
Question Bank - Module 3
 Mr. K B Hemanth Raj (Future Vision BIE)
March 15, 2020
Mr. K B Hemanth Raj (Future Vision BIE)
March 15, 2020
These Questions are being framed for helping the students in the "FINAL Exams" Only (Remember for Internals the Question Paper is set by your respective teachers). Questions may be repeated, just to show students how VTU can frame Questions.
- ADMIN
1. What is clipping? Explain with example the Sutherland-Hodgman polygon clipping algorithm. (08 Marks) (Dec.2019/Jan.2020)
2. Explain basic illumination models. (08 Marks) (Dec.2019/Jan.2020)
3. Explain RGB and CMY color models with examples. Explain the transformation between CMY and RGB color spaces. (08 Marks) (Dec.2019/Jan.2020)
4. Obtain the matrix representation for rotation of a object about an arbitrary axis. (08 Marks) (Dec.2019/Jan.2020)
5. Design a transformation matrix for window to viewport transformation. And explain how reshape function (glutReshapeFunc) works in openGL programming. (05 Marks) (June/July 2019)
6. With the help of a suitable diagram explain basic 3D Geometric transformation techniques and give the transformation matrix. Explain the meaning of affine transformation. (05 Marks) (June/July 2019)
7. With the help of openGL statements and diagram explain illumination and shading models. (06 Marks) (June/July 2019)
8. What is Clipping? With the help of a suitable example explain cohen Southerland line clipping algorithm. (06 Marks) (June/July 2019)
9. Design transformation matrix to rotate an 3D object about an axis that is parallel to one of the co-ordinate axes. (06 Marks) (June/July 2019)
10. With the help of a suitable diagram, explain basic illumination, RGB and CMY colour models. (04 Marks) (June/July 2019)
11. Define clipping. Briefly explain Co-hen Suterland line clipping without code. Discuss four cases. (10 Marks) (Dec.2018/Jan.2019)
12. Describe phong lighting model. (06 Marks) (Dec.2018/Jan.2019)
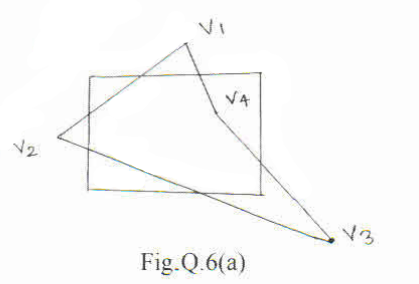
13. Clip the polygon given in Fig.Q.6(a), using Suterland Hodgman polygon clipping algorithm with neat sketches. (06 Marks) (Dec.2018/Jan.2019)
14. Explain the different types of light sources supported by OpenGl. (06 Marks) (Dec.2018/Jan.2019)
15. Explain the RGB and CMY color models. (04 Marks) (Dec.2018/Jan.2019)
16. Explain Cohen Sutherland line clipping clip the lines with coordinates (x0, y0) = (60, 20) (x1, y1) = (80, 120) given the window boundaries (Xwmin, Ywmin) = (50, 50) and (Xwmax, Ywmax) = (100, 100) (08 Marks) (June/July 2018)
17. Define color model. With neat diagram explain RGB and CMY color model. (08 Marks) (June/July 2018)
18. Explain Sutherland Hodgman Polygon clipping. Find the final clipped vertices for the following Fig Q6(a) (08 Marks) (June/July 2018)
19. Explain Specular Reflection and phong model. (08 Marks) (June/July 2018)
20. Define and represent the following #D transformation in homogeneous co-ordinates system:
I. Translation
II. Scaling (Dec.2016/Jan.2017 |10 Scheme)
21. What is concatenation of transformation? Explain 3D rotation about a fixed point. (10 Marks) (Dec.2016/Jan.2017 |10 Scheme)
22. Bring out the differences between perspective and parallel projections. (6 Marks) (Dec.2016/Jan.2017 |10 Scheme)
23. Explain the 2-buffer algorithm. (04 Marks) (Dec.2016/Jan.2017 |10 Scheme)
24. Derive the simple perspective projection matrix. (10 Marks) (Dec.2016/Jan.2017 |10 Scheme)
25. What care Affine transformation? Explain the basic affine transformation in 3D along with their matrix forms. (10 Marks) (June/July.2019 |10 Scheme)
26. What care Quaternions? With an example. explain how Quaternion are used in rotation in a 3D space. Give the mathematical representation of Quaternion. (10 Marks) (June/July.2019 |10 Scheme)
27. What are simple projections? Obtain perspective and orthogonal 4x4 matrix representation. (10 Marks) (June/July.2019 |10 Scheme)
28. Briefly explain the projections in openGL and demonstrate with the help of a suitable program. (10 Marks) (June/July.2019 |10 Scheme)
29. What is concatenation transformation? Explain rotation about a fixed point. (08 Marks) (Dec.2017/Jan.2018 |10 Scheme)
30. Explain how quaternions are used in rotation in a three-dimensional space. also list some of its advantages. (12 Marks) (Dec.2017/Jan.2018 |10 Scheme)
31. Explain the various types of views that are employed in computer graphics systems. (10 Marks) (Dec.2017/Jan.2018 |10 Scheme)
32. Explain glFrustrum( ) with syntax. (06 Marks) (Dec.2017/Jan.2018 |10 Scheme)
33. Define the term Axonometric projection, also list its types. (04 Marks) (Dec.2017/Jan.2018 |10 Scheme)
34. Obtain the matrix representation for rotation of a point about an arbitrary axis in a 3D space. (10 Marks) (June/July.2017 |10 Scheme)
35. Show that the following three dimensional sequences are commute:
I. A rotation and a uniform scaling.
II. Two rotations about the same axis. (10 Marks) (June/July.2017 |10 Scheme)